Modeling and Simulation of Microbial Enhanced Oil Recovery: A New Approach which Includes the Role of Interfacial Area, 2016
David Landa Marbán
Main content
Advisors: Florian Adrian Radu, Jan M. Nordbotten
Short description of project:
In today's world, oil remains the main source of energy. After discovering a petroleum reservoir, one can extract about 30% of the oil by using and maintaining the initial pressure in the reservoir through water ooding (first and second phase oil recovery). Nevertheless, 60-70% of oil remains in the reservoir after this, so called conventional recovery, so enhanced oil recovery (EOR) is strongly needed. Microbial enhanced oil recovery (MEOR) is an environmentally friendly and very promising EOR technology.
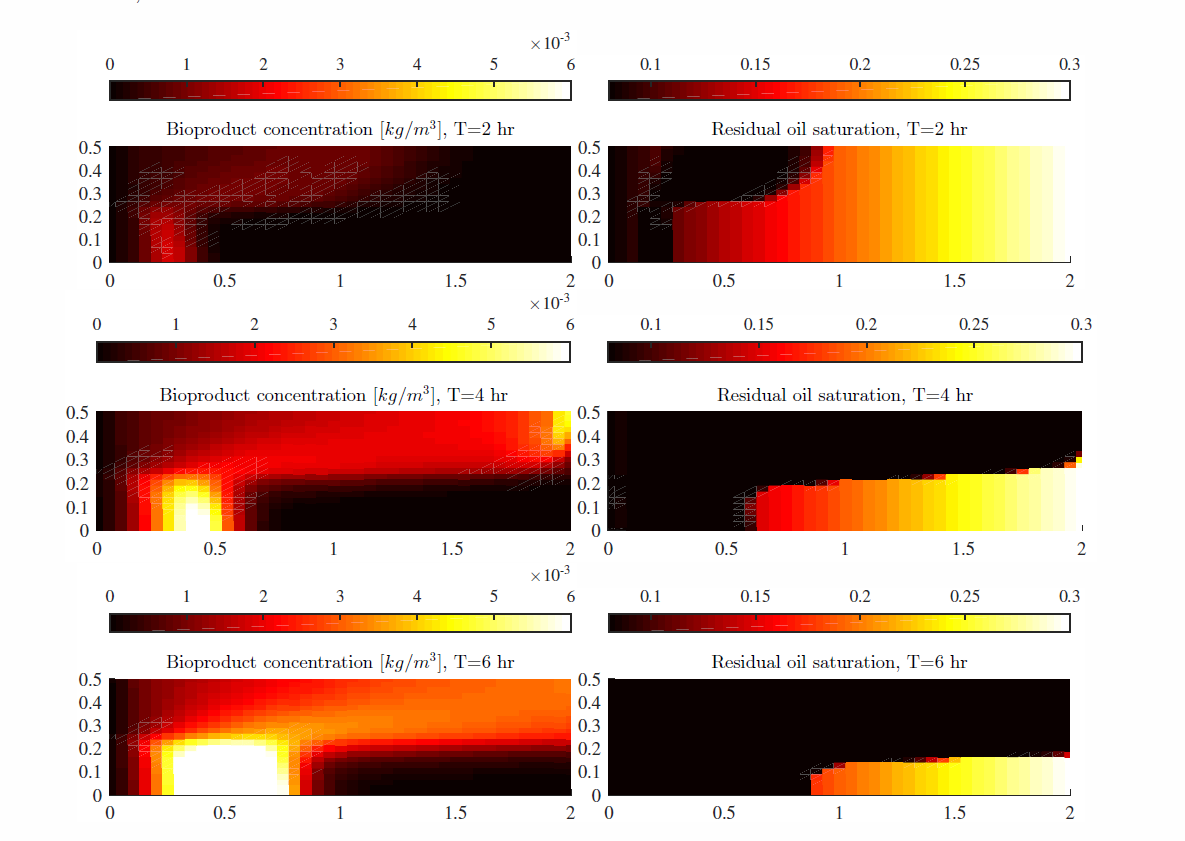
In this thesis we implement a non-standard model for MEOR that includes the interfacial area between the oil and water. We consider the two-phase ow equations and multicomponent reactive transport equations for three components: bacteria, nutrients and biosurfactants. The growth of bacteria affects the properties of the medium (porosity, permeability), up to the extreme case of pore clogging (bioclogging) and generation of new paths. Biosurfactants lower the interfacial tension, which improves the oil recovery. We consider in this thesis, for the fi The motivation to include the interfacial area in the model is to eliminate the hysteresis in the capillary pressure relationship and model that biosurfactants are mainly living at the oil-water interface.
A typical mathematical model for MEOR consists on nonlinear coupled partial differential equations (PDEs) and ordinary differential equations (ODEs). The spatial discretization is obtained using finite differences (FD) and two-point ux approximation (TPFA), and the time discretization using backward Euler (BE). We make the implementation for 1-D and 2-D domains using cell-centered grids. We present in detail the discretization of the equations, including the treatment of the boundary conditions. After the discretization in space and time, the problems to be solved at each time step are still nonlinear. For solving these equations, we use an implicit scheme that considers a linear approximation of the capillary pressure gradient, which results in an efficient and stable scheme. The code for running the simulations is written in MATLAB. Following this, we test the code with analytic solutions and benchmark simulations.
We consider a 1-D porous medium where we study the spatial distribution and the evolution in time of the average pressure, water saturation, oil-water interfacial area, capillary pressure, porosity, permeability ratio, residual oil water saturation and bacterial, nutrient and biosurfactant concentrations. After, we make a sensitivity analysis in order to examine the effects of the relevant model parameters. Finally, we make simulations considering a porous medium with a thief zone, which is a 2-D problem.
A comprehensive model, including two-phase ow, bacteria, nutrients and biosurfactants was implemented. The model has been tested using analytic and benchmark problems. For the first time, the role of interfacial area in MEOR was studied. We showed that different predictions of oil recovery are obtained by including the availability of interfacial area in the model. Nevertheless, it is necessary to do more experiments in the laboratory in order to compare with the numerical simulations and validate the model assumptions.
Link to thesis at BORA-UiB: http://dspace.uib.no/handle/1956/12297