Preconditioning for Flow in Fractured Porous Media, 2020
Ana Budiša
Main content
Advisors: Eirik Keilegavlen, Florin Radu and Jan Martin Nordbotten
Short description of project:
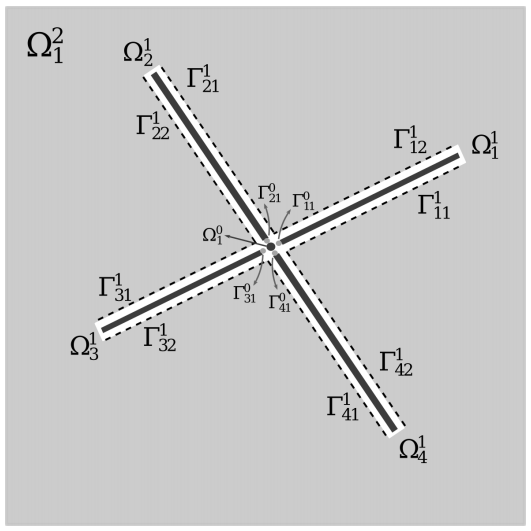
The key to reliable simulations of flow in fractured porous media is the proper design, analysis and implementation of numerical methods. These methods should take into account the specific properties of the underlying model, while at the same time be flexible enough to handle variability of the model's components. The particular features of fractured porous media we concern ourselves with are the complex geometry of the fracture network and the disparity in scales in the model parameters. The model we study is based on interpretation of fractures and the porous rock as a mixed-dimensional geometry, and the resulting system of partial differential equations is highly coupled and parameter-dependent. In this thesis, we build upon the common approaches to discretization of the flow problem and deliver a numerical solution by constructing efficient numerical solvers and preconditioners. The two main topics of our research are the design of preconditioners to finite element discretization of the linear flow model and the development of linearization methods to the non-linear model.
In the first part, we consider the fact that our flow problem reveals the saddle-point structure. This motivates to see how some established approaches to preconditioning saddle-point problems work under the mixed-dimensional complexity. We construct the preconditioners to the classical solving approaches, such as Krylov subspace methods, based on the well-posedness of our saddle-point system. As the goal of any preconditioner is to approximate the inverse of the coefficient operator of the system, the principal idea of our approach is to find that inverse mapping that is equivalent in terms of norms on the given function spaces. In this way, we can ensure that the preconditioned numerical solvers will converge more rapidly, independently of values of the discretization and physical parameters. In our case, we are able to derive two such preconditioners by identifying two different topologies on the given discrete finite-element spaces. In fact, one of the approaches leads to a general framework to preconditioning mixed-dimensional elliptic problems that can be applied to other problems with a similar hierarchical structure as the model of flow in fractured porous media.
Finally, we study a choice of non-linear and time-dependent flow models that appear in cases of enhanced conductivity of the fractures and compressibility of the fluid. The development of the iterative solution methods for our problem considers the natural domain decomposition setting imposed by the fracture network and the standard linearization methods are adapted to the mixed-dimensional setting. By using non-matching grids, we can employ a multiscale method to the interface problem to handle the dominating computational cost in each iteration of the non-linear solver, namely the repeated solving process on the rock matrix subdomains. The flexibility of the method is showcased by successfully applying it to several non-linear flow models.
Link to thesis at BORA-UiB: http://bora.uib.no/handle/1956/21389