On the optimization of iterative schemes for solving non-linear and/or coupled PDEs, 2018
Erlend Storvik
Main content
Advisors: Florin Radu and Erlend Storvik
Short description of the project:
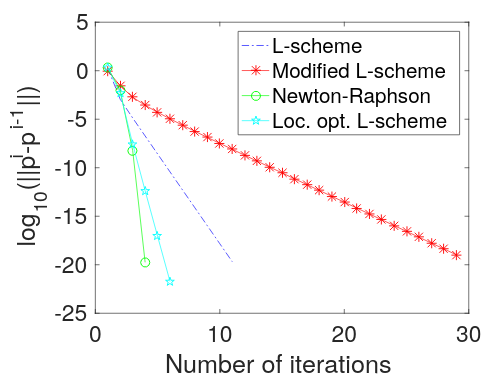
In this thesis, we study the optimization of iterative schemes as both linearization methods, and as splitting methods for solving non-linear and coupled partial differential equations (PDEs). We consider two equations that are describing processes in porous media; Richards’ equation, a possibly degenerate, non-linear, and elliptic/parabolic equation that models the flow of water in saturated/unsaturated porous media, and Biot’s equations, a coupled system of equations that models flow in deformable porous media. For Richards’ equation, we compare the numerical properties of several linearization schemes, including the Newton-Raphson method, the modified Picard method, and the L-scheme. Additionally, we prove convergence of the linearly and globally convergent L-scheme and discuss theoretically and practically how to choose its stabilization parameter optimally in the sense that convergence is obtained in the least amount of iterations. The second aim of the thesis is to effectively solve the quasi-static, linear Biot model. We consider the fixed-stress splitting scheme, which is a popular method for iteratively solving Biot’s equations. It is well-known that the convergence of the method is strongly dependent on the applied stabilization parameter. We propose a new approach to optimize this parameter and show theoretically that it does not only depend on the mechanical properties and the coupling coefficient, but also on the fluid’s flow properties. The type of analysis presented in this thesis is not restricted to a particular spatial discretization, but we require it to be inf-sup stable. The convergence proof also applies to low-compressible or incompressible fluids and low-permeable porous media. We perform illustrative numerical examples, including a well-known benchmark problem, Mandel’s problem. The results largely agree with the theoretical findings. Furthermore, we show numerically that for conditionally inf-sup stable discretizations, the performance of the fixed-stress splitting scheme behaves in a manner that contradicts the theory provided for inf-sup stable discretizations.
Link to the thesis at BORA: https://bora.uib.no/bora-xmlui/handle/1956/18755