Fast integral equation methods for seismic wavefield modelling in complex media

Project description
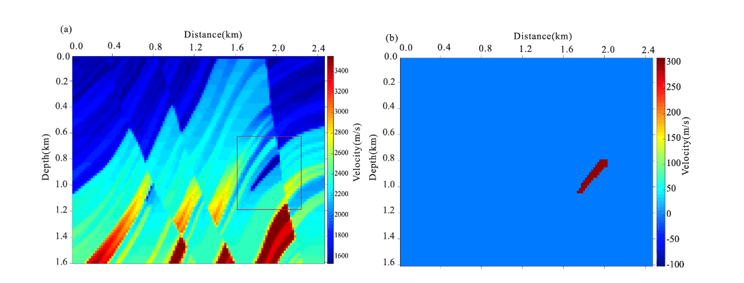
This project focus on the development of fast integral equation methods for seismic wavefield modelling in complex media (e.g., involving salt structures, faults and/or curved layers). Such methods are highly relevant for seismic monitoring of CO2 storage and geothermal energy production in addition to traditional petroleum seismology; and can in principle also be applied to medical imaging.

Integral equation methods are based on a decomposition of the actual medium (seismic velocity model) into a background medium and a corresponding scattering potential model (anomaly). Integral equation methods calculate the full wavefield and is thus suitable for seismic full-waveform inversion; which represents the state-of-the-art within seismic imaging.

Integral equation methods has several advantages and some disadvantages compared with traditional numerical methods such as the finite difference methods.

A significant advantage of the integral equation approach is that one can focus the wavefield modelling (and inversion) on a target of interest and absorb the rest of the model into the background model. Thus, integral equation approach is highly suitable for 4D seismic or time-lapse studies (Huang et al., 2019; Huang, 2020).

The fact that the computational cost and memory requirements of the integral equation approach is relatively high compared with the finite difference method has traditionally been regarded as a disadvantage. However, we have recently developed several methods for speeding up the integral equation methods and also to reduce the memoryrequirements (Jakobsen et al., 2020).

The main goal of this project is to develop fast integral equation methods based on the Fast Fourier Transform (FFT) algorithm and special methods for ensuring that iterative solutions of the integral equations converges. Numerical experiments shall be performed for large 2D or 3D models. Depending on the interest and progress of the student, this project can also involve some work on seismic full waveform inversion (Jakobsen, 2018).

References
Jakobsen M., Wu R. S. and Huang. X., 2020.
Convergent scattering series solution of the inhomogeneous Helmholtz equation via renormalization group and homotopy continuation approaches. Journal of Computational Physics, 109343

Huang X., Jakobsen M.,
Eikrem K. S. and Nævdal G., 2019. Target-oriented inversion of time-lapse seismic waveform data. Communication in Computational Physics, doi: 10.4208/cicp.OA-2018-0143.

Jakobsen, M. and Wu, R.S., 2018. Accelerating the T-matrix approach to seismic full-waveform inversion by domain decomposition. Geophysical Prospecting, 66, 1039-1059.

Proposed course plan during the master's degree (60 ECTS):
GEOV218 Rock physics
GEOV276 Introduction to theoretical seismology
GEOV277 Signal and inversion theory in earth science
MAT212 Multivariable calculus

Prerequisites:
An interest in mathematical modelling and programmingin addition to geophysics.

Felt- lab- og analysearbeid
Numerical analysis only.