Anvendelser
Problemer og dype matematiske teorier som i utgangspunktet ble studert uten tanke på praktiske anvendelser, har vist seg å bli helt avgjørende i praktiske sammenhenger mange tiår senere.
Hovedinnhold
Tallteori ble frem til 60-tallet sett på som rent tankespinn, men er idag selve byggesteinen for all overføring av sikker informasjon, nærmere bestemt i fagfeltene kryptografi og kodeteori. Dette brukes hver gang du drar bankkortet eller sender en e-post.
Boolsk algebra, utviklet rent abstrakt av George Boole i 1854, har funnet praktiske anvendelsesområder innenfor digitalteknikk og styringsteknikk.
En del av geometrien kalt projektiv geometri, som beskjeftiger seg med punkter og linjer "i det uendelige", ble utviklet på 1800-tallet og er idag en hjørnestein i "computer vision", som f.eks. brukes til å programmere bevegelser av roboter.
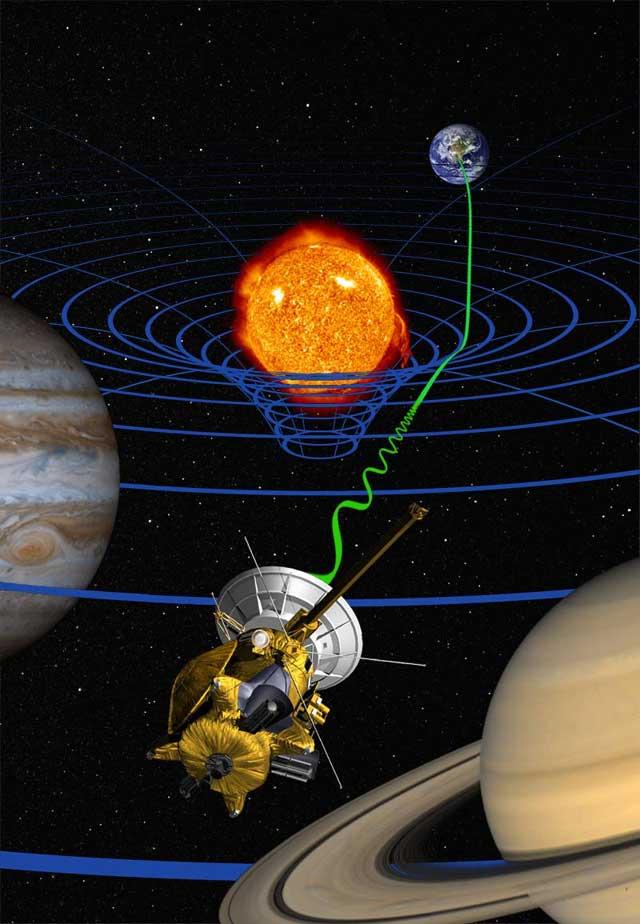
En annen type geometri kalt differensialgeometri beskjeftiger seg med begreper som avstand og arealer i krummede rom og ble utviklet tidlig på 1800-tallet i forbindelse med jordmålinger og kartproduksjon. Gjennom hele 1800-tallet ble feltet utviklet videre som et eget rent teoretisk fagfelt og dette ble et helt avgjørende fundament i Einsteins generelle relativitetsteori. Einsteins teorier baserte seg dessuten i stor grad fra tanker fra ikke-euklidsk geometri, kort sagt "geometri der rette linjer erstattes av krummede", som på kuleflaten, utviklet på 1800-tallet.
Fagfeltet kalt topologi studerer egenskaper av "rom" som er bevart ved deformasjoner. Det berømte matematiske problemet om de syv broene i Königsberg er et av de problemene som har formet fagfeltet. Leonhard Eulers løsning fra 1736 ble videre utviklet de etterfølgende århundrene og topologi er idag avgjørende for teorier i teoretisk fysikk som ormehull og strengteori. Ormehull er det som gjør det teoretisk mulig å "hoppe" fra ett sted til et annet i rommet. Strengteori er en matematisk-fysisk teori som har som mål å forklare alle naturfenomer og hele vårt univers med en enhetlig teori. Her går man ut fra at elementærpartiklene ikke er punktpartikler, men strenger som beveger seg i et 10-dimensjonalt univers. Fire av disse er rom-tid-dimensjonene vi ser til daglig, og de resterende seks er knøttsmå "sammenkrøllede" dimensjoner som viser seg å måtte ha helt bestemte matematiske egenskaper, nemlig egenskapene til bestemte typer rom som rene matematikere hadde studert siden 50-tallet og som hadde fått navnet Calabi-Yau mangfoldigheter. Strenger i bevegelser i disse skjulte dimensjonene maler ut flater som kalles Riemannske flater etter den tyske matematikeren Bernhard Riemann og studiet av Riemannske flater i Calabi-Yau mangfoldigheter er et sentralt tema i fagfelt i ren matematikk kalt analytisk geometri og algebraisk geometri.