Hva er algebraisk geometri?

Algebraisk geometri har en lang historie som kan sies å gå tilbake til den euklidske geometrien i antikkens Hellas. En milepæl var Descartes' innføring av koordinater i geometrien. Dette førte til at man kunne gå fram og tilbake mellom en algebraisk behandling av ligninger for et geometisk objekt og et direkte geometrisk studium av objektet. Idag er algebraisk geometri et område innenfor geometri med forbindelser til andre områder som kommutativ algebra, kompleks analyse, topologi og tallteori innefor matematikk, kryptografi i informatikk og strengteori innenfor fysikk.

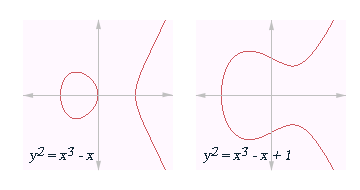
Objektene vi studerer i algebraisk geometri er algebraiske varieteter, som vi kan si er geometriske objekter som kan defineres ved løsningsmengdertil polynomer. For eksempel kan den to-dimensjonale sfæren i det tredimensjonale euklidske rommet R³ defineres som mengden av alle punkter (x,y,z) som tilfredsstiller x2+y2+z2-1=0.

Ser vi videre på alle punkter som tilfredsstiller de to ligningene x2+y2+z2-1=0, x+y+z=0 da får vi den sirkelen på skrå på kuleflaten markert med rødt på figuren.

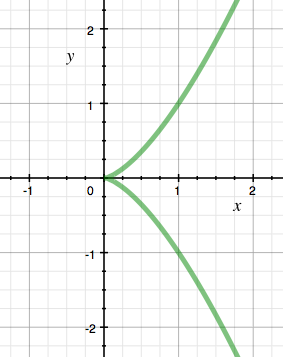
På den annen side er moderne algebraisk geometri ikke så opptatt av selve ligningene som beskriver objektene, men konsentrerer seg om de abstrakte egenskaper til de geometriske objektene ved å tilordne dem algebraiske strukturer. Oversettelsen til agebra gjør at algebraisk geometri egner seg til å studere geometriske problemer av høyere kompleksitet enn nærliggende fagfelt. Dette gjelder ikke minst studiet av singulære punkter på geometriske objekter, grovt sagt punkter der objektet ikke er "glatt". Et klassisk eksempel er origo på kurven definert ved ligningen x3-y2=0.

Noen problemer innenfor algebraisk geometri går flere hundre å tilbake i tid, samtidig som algebraisk geometri brukes til å løse gamle problemer. Dette er tilfellet med Fermats siste sats, det kanskje mest berømte matematiske problemet i historien. I 1637 formulerte den franske matematikerenPierre de Fermat følgende sats:

Hvis et heltall n er større enn 2, da har ligningen a ⁿ + b ⁿ = c ⁿ ingen løsninger blant hele tall a, b og c forskjellig fra null.

Fermat skrev "Jeg har et virkelig flott bevis for denne satsen som margen er for liten til å kunne inneholde". Etter Fermats levetid forsøkte flere og flere matematikere å finne et bevis for denne satsen, men det viste seg å være vanskelig. Problemet, om enn så enkelt å formulere, utviklet seg til et av de mest intrikate og enigmatiske problemene som noen gang har blitt skapt. Et enormt antall gale bevis for satsen har blitt produsert. Et korrekt bevis, ble funnet etter 357 år, i 1995, av den engelske matematikeren Sir Andrew Wiles, og involverer blant annet algebraisk geometri, spesieltelliptiske kurver, spesielle type kurver som har blitt studert i mange hundre år.

Samtidig har algebraisk geometri vist seg å være et effektivt verktøy for å løse eller formulere problemer innenfor andre vitenskaper. Problemer og teorier som i utgangspunktet ble studert uten tanke på praktiske anvendelser, har vist seg å bli helt avgjørende i praktiske sammenhenger mange tiår senere. Viktige eksempler på anvendelser er innenfor kryptografi og kodeteori, som brukes til all overføring av sikker informasjon,. Dette brukes hver gang du drar bankkortet eller sender en e-post.

En del av den algebraiske geometrien kalt projektiv geometri, som beskjeftiger seg med punkter og linjer "i det uendelige", ble utviklet på 1800-tallet og er idag en hjørnestein i "computer vision", som f.eks. brukes til å programmere bevegelser av roboter.

Klassiske algebraisk-geometriske objekter som har blitt studert siden 1800-tallet i "den italienske skolen i geometri" har vist seg å dukke opp ifylogenetikk, som er den delen av evolusjonsbiologien som rekonstruerer slektskapsforholdene mellom arter.

Strengteori er en matematisk-fysisk teori som har som mål å forklare alle naturfenomer og hele vårt univers med en enhetlig teori. Her går man ut fra at elementærpartiklene ikkke er punktpartikler, men strenger som beveger seg i et 10-dimensjonalt univers. Fire av disse er rom-tid-dimensjonene vi ser til daglig, og de resterende seks er knøttsmå "sammenkrøllede" dimensjoner som viser seg å måtte ha helt bestemte matematiske egenskaper, nemlig egenskapene til bestemte typer rom algebraiske geometere hadde studert siden 50-tallet og som hadde fått navnetCalabi-Yau mangfoldigheter. Strenger i bevegelser i disse skjulte dimensjonene maler ut flater som kalles Riemannske flater etter den tyske matematikeren Bernhard Riemann og studiet av Riemannske flater i Calabi-Yau mangfoldigheter er et sentralt tema i algebraisk geometri, også blant medlemmene i gruppen vår.

Vi tilbyr både undervisning og mastergradsveiledning i algebrasik geometri. Våre forskningsinteresser, og dermed også temaer for masteroppgaver, går fra klassiske problemer til matematikken knyttet til strengteori. Algebraisk geometri kan derfor også være riktig valg av stidium for deg som er interessert i teoretisk fysikk.

Interessert? Kontakt ALK.