Mathematical and Numerical Analysis of Flow in Deformable Porous Media, 2019
Jakub Wiktor Both
Main content
Advisors: Florin Adrian Radu, Kundan Kumar and Jan Martin Nordbotten
Short description of project:
This dissertation focuses on the mathematical analysis and numerical solution of coupled deformation- and flow-related processes in porous media, modeled by the theory of poro-elasticity. It comprises contributions within three topics: the gradient flow structures of quasi-static thermo-poro-visco-elastic processes in porous media; the numerical analysis and fine-tuning of the fixed-stress split for Biot's consolidation model; and the well-posedness analysis and robust solution of unsaturated poro-elasticity.
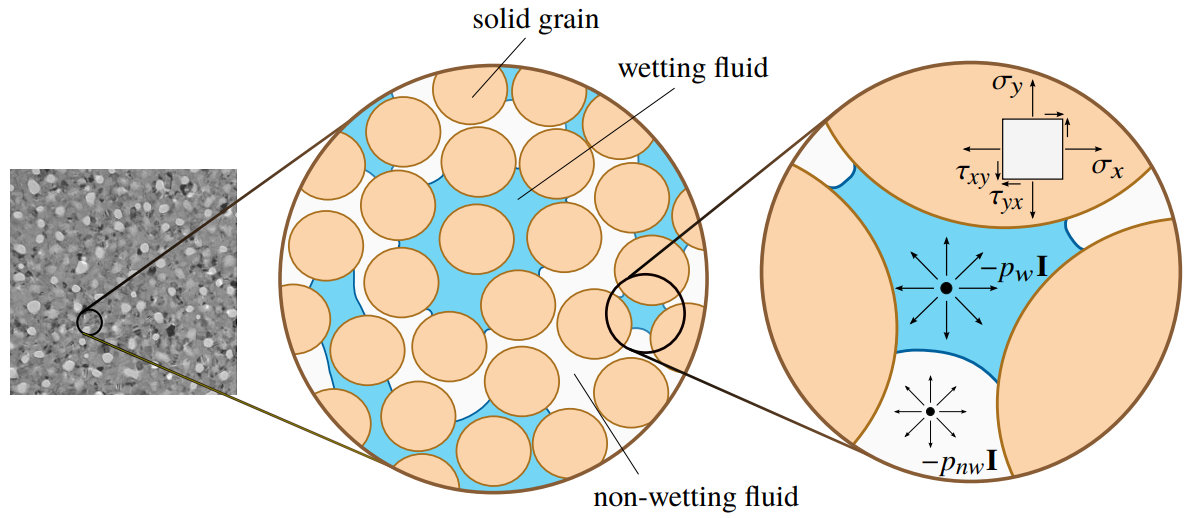
The fluid-structure interaction of fluids and porous solid materials is of great relevance for various applications within geotechnical, reservoir, structural, and biomedical engineering. Depending on the application different characteristics of a poro-elastic system may be relevant. In order to correctly predict such complex systems, accurate well-posed models are needed - as well as their robust numerical solution. As part of this thesis, a unified gradient flow framework is established for the modelling of coupled hydro-mechanical processes in porous media driven by the dissipation of energy. By involving thermodynamic knowledge, it allows for instance for the modelling of non-linearly compressible single-phase flow or non-Darcy flow within a non-linearly elastic (but geometrically linear) or visco-elastic, solid matrix - besides classical, linear poro-elasticity. The framework lays a foundation for the unified mathematical and numerical analysis of these models. In particular, well-posedness is established based on the abstract theory of doubly non-linear evolution equations. Furthermore, block-partitioned iterative solvers, exploiting the inherent block structure of coupled problems, are naturally developed by means of block-coordinate descent methods (with optional line search) for block-separable minimization problems, arising from the discretization of gradient flow formulations. Those are equipped with strong robustness properties under mild conditions, and allow for exploiting tailored, individual solver technology for the physical subproblems. On the one hand, the framework covers well-established theory fortifying its capability. For instance, applied to Biot's consolidation model, the widely-used fixed-stress split arises naturally, and guaranteed convergence rates consistent with the literature are derived. On the other hand, novel splitting schemes with guaranteed convergence rates are determined for more involved models as, e.g., linear poro-visco-elasticity. After all, the methodology applies equally to linear as to non-linear problems.
Biot's quasi-static consolidation model constitutes the simplest coupled model accounting for single-phase flow in a linearly elastic porous medium. At the same time it represents the prototype for any coupled poro-elasticity model. Consequently, a thorough understanding of this simple model is required in order to optimally solve more involved models. In this thesis, we gain deeper theoretical and practical understanding of the popular fixed-stress split for Biot's quasi-static consolidation model. More precisely, we consider a fixed-stress split with variable stabilization allowing for tuning the performance. Parameter-robust convergence of the splitting scheme is established for fully heterogeneous media. Furthermore, influences on the practically optimal stabilization parameter, leading to a minimal number of iterations, are practically and theoretically identified. The studies suggest that the optimal stabilization parameter does not only depend on mechanical and coupling material parameters as found in the literature. Instead, it also depends on fluid flow parameters, the stability of the spatial discretization, the computational domain, and boundary conditions. Alternatively to tuning the performance (or in addition), relaxation can be applied as, e.g., line search, based on the gradient flow structure of poro-elasticity.
The model for unsaturated poro-elasticity is a non-linear extension of Biot's quasi-static consolidation model. It results from the reduction of the general model for two-phase flow in deformable porous media to the unsaturated zone, i.e., effectively one fluid phase is simply neglected. Typical examples, in which this simplification is acceptable, origin from geotechnical engineering and building engineering, e.g., the stability analysis of dikes, or the drying shrinkage and cracking of cement. In this dissertation, unsaturated poro-elasticity is studied from two perspectives, constituting a step towards a better mathematical and numerical understanding of multi-phase flow in deformable porous media. First, the existence of weak solutions is established. Second, a robust block-partitioned linearization is provided, based in the fixed-stress split, and convergence is theoretically proved. Further acceleration is proposed using the Anderson acceleration, complying with the block-partitioned character of the solver. Theoretical justification is also provided for the Anderson acceleration to both accelerate contractive fixed point iterations, and to increase the robustness of non-contractive fixed point iterations. Thereby, the Anderson acceleration constitutes an adequate alternative to line search techniques - in particular in the context of non-linear, block-structured problems.
Link to thesis at BORA-UiB: http://bora.uib.no/handle/1956/21151